Số chính phương là gì? Một số ví dụ số chính phương dễ hiểu

Các bạn đang tìm hiểu về số chính phương là gì trong toán học? Vậy mới các bạn cùng tham khảo bài viết dưới đây để hiểu rõ về khái niệm của số chính phương và có ví dụ rõ ràng để các bạn nhận biết và tính toán số chính phương như thế nào là chính xác.

Số chính phương là gì?

Số chính phương là số tự nhiên có căn bậc 2 là một số tự nhiên. Số chính phương bản chất là bình phương của một con số tự nhiên nào đó. Số chính phương còn là diện tích của một hình vuông với cạnh là số nguyên kia.

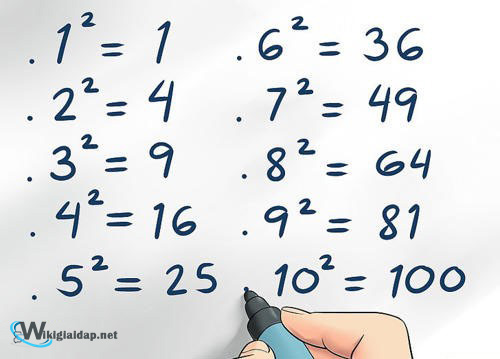
Một con số được gọi là số chính phương chẵn nếu như nó là bình phương của một số chẵn. Và ngược lại, một con số chính phương được gọi là số chính phương lẻ nếu như nó là bình phương của một con số lẻ bất kỳ.

Tính chất của số chính phương

Một con số được xem là số chính phương chỉ có những chữ số tận cùng là 0,1,4,5,6,9, còn đối với các con số tận cùng là số 2,3,7,8 thì không phải là số chính phương nhé các bạn.

Khi chúng ta phân tích ra thừa số nguyên tố, số chính phương hoàn toàn chỉ chứa những thừa nguyên tố với số mũ chẵn, không có mũ lẻ.

• Số chính phương chỉ có 1 trong 2 dạng là 4n hoặc là 4n + 1, 3n hoặc 3n + 1, chứ không có số chính phương nào có dạng là 4n + 2 hay là 4n + 3, 3n + 2,…
• Số chính phương có chữ số tận cùng là số 1 hoặc là số 9 thì chữ số hàng chục sẽ là chữ số chẵn.
• Số chính phương tận cùng nếu bằng 5 thì chữ số hàng chục sẽ là 2.
• Số chính phương tận cùng nếu bằng 4 thì chữ số hàng chục sẽ là chữ số chẵn.
• Số chính phương tận cùng bằng 6, chữ số hàng chục sẽ là chữ số lẻ.
• Số chính phương chia hết cho 2 thì sẽ chia hết cho 4.
• Số chính phương chia hết cho 3 thì tất nhiên sẽ chia hết cho 9.
• Số chính phương chia hết cho số 10 thì sẽ chia hết cho 20.
• Số chính phương chia hết cho 5 thì sẽ chia hết cho 15.

Còn số chính phương mà chia hết cho 3 thì không bao giờ có số dư là 2; chia hết cho 4 thì không bao giờ dư 2 hoặc 3; số chính phương lẻ chia hết cho số 8 luôn luôn dư 1.

Ví dụ:

4(2)2; 9(3)2; là những số chính phương.

Công thức để tính hiệu của hai số chính phương là:

a2 – b2 = (a + b)(a – b).

Ví dụ:

42 – 32 = (4 + 2)(4 – 2) = 12.

Số ước nguyên dương của số chính phương là một con số chẵn.

Số chính phương chia hết cho số nguyên tố p thì chắc chắn sẽ chia hết cho p2.

Ví dụ:

Số chính phương là 12 (24) chia hết cho 2 (12:2=6) => 12 cũng sẽ chia hết cho 4 (12:4=3)

Số chính phương 144 (122) chia hết cho 3 (85) => 144 cũng chia hết cho 9 (16)

Tất cả những số chính phương có thể viết thành một dãy số tổng của các số lẻ tăng dần theo thứ tự từ 1 = 1; 4 = 3 + 1; 9 = 1 + 3 + 5, 16 = 1 + 3 + 5 + 7; 25 = 1 + 3 + 5 + 7 + 9; 37 = 1 + 3 + 5 + 7 + 9 + 12,…

Ví dụ số chính phương

Dựa theo khái niệm và tính chất trên, ta có một vài ví dụ về số chính phương như sau:

Các con số từ 4, 9, 16, 25, 36, 49, 64, 81, 144, 225, 576 đều là số chính phương.

• Số 4 = 22 là số chính phương chẵn
• Số 9 = 32 là số chính phương lẻ
• Số 16 = 42 là số chính phương chẵn
• Số 25 = 52 là số chính phương lẻ
• Số 36 = 62 là số chính phương chẵn
• Số 225 = 152 là số chính phương lẻ
• Số 289 = 172 là số chính phương lẻ
• Số 576 = 242 là số chính phương chẵn
• Số 1.000.000 = 1.0002 là số chính phương chẵn

Một số bài toán mẫu về số chính phương

Bài toán mẫu 1: Chứng minh một số không phải là số chính phương.

Ví dụ 1: Chứng minh số n = 20042 + 20032 + 20022 – 20012 không phải là số chính phương.

Giải đáp: Có thể nhận thất chữ số tận cùng của những số 20042, 20032, 20022, 20012 lần lượt là số 6,9,4,1. Vì thế số n có chữ số tận cùng là 8, nên n không phải là số chính phương.

Ví dụ 2: Chứng minh số 1234567890 không phải là số chính phương.

Giải đáp: Ta có thể thấy số 1234567890 đều chia hết cho 5 vì chữ số tận cùng là 0. Nhưng lại không chia hết cho số 25 vì hai chữ số tận cùng của dãy số là 90. Do đó mà số 1234567890 không phải là số chính phương.

Bài toán mẫu 2: Chứng minh một số là số chính phương

Chứng minh: Với mọi số tự nhiên n thì an = n(n+1)(n+2)(n+3) + 1 là số chính phương.

Giải đáp:

Ta có:

an = n(n+1)(n+2)(n+3) + 1

= (n2 + 3n)(n2 + 3n + 2) +1

= (n2 + 3n)2+ 2(n2 + 3n) + 1

= (n2 + 3n + 1)2

Trong đó: n là số tự nhiên thì (n2 + 3n + 1)2 cũng là một số tự nhiên, vì vậy, an là số chính phương.

Trên đây là bài viết chia sẻ đến các bạn đọc về số chính phương là gì? Một số ví dụ số chính phương dễ hiểu. Hy vọng sau khi đọc qua bài viết này của wikigiaidap.net các bạn sẽ hiểu rõ hơn về số chính phương, để giải quyết các bài toán có liên quan đến số chính phương một cách tốt nhất và chính xác nhất nhé. Chúc các bạn thành công!